طریقه نمره گذاری و تحلیل آزمون و کارنامه های بدون غلط در برنامه تصحیح تست هوشمند آسا
فهرست
- محاسبه نمره خام هر درس
- محاسبه ی نمره معیار هر درس در آزمون
- محاسبه نمره تراز
- نمودار (توزیع) نرمال
- محاسبه تراز کلی هر شرکت کننده
- مفهوم تراز
- ضریب دشواری
- ضریب تمییز
- کارنامه بدون غلط / کارنامه های بدون غلط
-
محاسبه نمره خام هر درس
در نمره گذاری آزمون های تستی در برنامه به روش زیر عمل می کنیم:
- شمارش تمام پاسخ های صحیح ( آن را C می نامیم)
-
به ازای هر 3 پاسخ غلط یک پاسخ صحیح حذف می شود. در برنامه این امکان وجود دارد که
به ازای هر 3، 4، 5 و یا 6 پاسخ غلط یک پاسخ صحیح حذف شود.
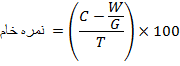
تعداد کل سوال ها:T
تعداد پاسخ های غلط: W
تعداد پاسخ های درست: C
حذف پاسخ درست به ازای G پاسخ غلط. در این برنامه پیش فرض 3 می باشد که قابل تغییر است.
-
محاسبه ی نمره معیار هر درس در آزمون
نمرات معیار، عملکرد هر شرکت کننده را در یک آزمون، بنا بر اختلاف عملکرد او از میانگین گروه، برحسب واحد انحراف معیار نشان می دهد. آن دسته از نمرات معیار که دارای توزیعی با میانگین صفر و انحراف معیار واحد هستند، به نمرات Z شهرت دارند.
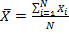
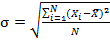
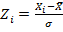
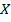 : نمره خام
: نمره خام
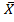 : میانگین نمرات خام
: میانگین نمرات خام
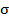 : انحراف از معیار نمرات
: انحراف از معیار نمرات
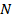 : تعداد نمرات شرکت کنندگان
: تعداد نمرات شرکت کنندگان
-
محاسبه نمره تراز
مقیاس نمرات (نمره تراز) T با ضرب نمرات (نمره معیار) Z در عدد ثابت a و جمع کردن نمرات حاصل با عدد ثابت b بدست می آید. بنابراین، آن دسته از نمرات معیار که دارای توزیعی با میانگین b و انحراف معیار a است، توزیع نمرات T نام دارد.
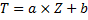
a = ضریب تراز = انحراف معیار
b = میانگین = ثابت تراز
ضرایب دانشگاه سراسری
2000
5000
ضرایب دانشگاه آزاد
2500
5000
ضرایب هماهنگ مدارس
1000
5000
ضرایب حدی 1
900
5000
ضرایب حدی 2
800
5000
ضرایب حدی 3
700
5000
ضرایب حدی 4
500
5000
-
نمودار (توزیع) نرمال
توزیع نرمال ، یکی از مهمترین توزیعهای احتمالی پیوسته در نظریه احتمالات است. علت نامگذاری و همچنین اهمیت این توزیع، همخوانی بسیاری از مقادیر حاصل شده، هنگام نوسانهای طبیعی و فیزیکی پیرامون یک مقدار ثابت با مقادیر حاصل از این توزیع است (در این جا میانگین آزمون می باشد). دلیل اصلی این پدیده، نقش توزیع نرمال در قضیه حد مرکزی است. به زبان ساده، در قضیه حد مرکزی نشان داده میشود که تحت شرایطی، مجموع مقادیر حاصل از متغیرهای مختلف که هرکدام میانگین و پراکندگی متناهی دارند، با افزایش تعداد متغیرها، دارای توزیعی بسیار نزدیک به توزیع نرمال است. این قانون که تحت شرایط و مفروضات طبیعی نیز برقرار است، سبب شده که برآیند نوسانهای مختلفِ تعداد زیادی از متغیرهای ناشناخته، در طبیعت به صورت توزیع نرمال آشکار شود. بعنوان مثال، با اینکه متغیرهای زیادی بر میزان خطای اندازهگیریِ یک کمیت اثر میگذارند، (مانند خطای دید، خطای وسیله اندازهگیری، شرایط محیط و ...) اما با اندازهگیری های متعدد، برآیند این خطاها همواره دارای توزیع نرمال است که حول مقدار ثابتی پراکنده شده است.مثالهای دیگری از این نوسانهای طبیعی، طول قد، وزن یا بهره هوشی افراد است
این توزیع گاهی به دلیل استفاده کارل فردریک گاوس از آن در کارهای خود با نام توزیع یا تابع گوسی (گاوسی) نامیده میشود؛ همچنین به دلیل شکل تابع احتمال این توزیع، با نام انحنای زنگولهای (زنگدیس) نیز معروف است

قسمت آبی تیره در فاصله یک برابر انحراف معیار از میانگین توزیع قرار دارد و قسمت آبی روشن و آبی تیره به طور توام، در فاصله دو برابر انحراف معیار از میانگین توزیع قرار دارند. در توزیع نرمال، اولی برابر با ۶۸٪ سطح زیر نمودار و دومی برابر با ۹۵٪ سطح زیر نمودار است
خصوصیات نمودار نرمال
- دو قسمت منحنی نرمال نسبت به خط وسط آن قرینه هستند.
- در توزیعی که این منحنی مُعرف آن است، اکثر نمره ها در وسط توزیع متمرکز شده اند.
- هرچه از وسط منحنی به دو طرف آن پیش برویم، از ارتفاع منحنی (حجم نمرات) کاسته می شود و در انتهای منحنی دنباله های طویلی به وجود می آیند.
- دو امتداد منحنی در بی نهایت محور افقی را قطع می کنند، زیرا تعداد مواردی که لازم است تا یک منحنی نرمال واقعی درست شود، از لحاظ نظری بی نهایت است.
- در منحنی نرمال، میانگین، میانه و نما بر روی هم قرار دارند.
- در روی این منحنی دو نقطه وجود دارد که در آن جهت منحنی تغییر می کند(نقطه عطف). این دو نقطه در فواصل ±1 انحراف معیار (σ) از میانگین قرار دارند.
-
محاسبه تراز کلی هر شرکت کننده
در صورتیکه
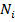 نمرات تراز دروس عمومی و
نمرات تراز دروس عمومی و
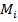 نمرات تراز دروس اختصاصی، وj تعداد دروس عمومی، و k تعداد دروس اختصاصی، و
نمرات تراز دروس اختصاصی، وj تعداد دروس عمومی، و k تعداد دروس اختصاصی، و
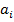 ضرایب دروس عمومی، و
ضرایب دروس عمومی، و
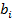 ضرایب دروس اختصاصی و c ضریب دروس عمومی و d ضریب دروس اختصاصی
باشد، نمره تراز کلی هر شرکت کننده از رابطه زیر محاسبه می شود:
ضرایب دروس اختصاصی و c ضریب دروس عمومی و d ضریب دروس اختصاصی
باشد، نمره تراز کلی هر شرکت کننده از رابطه زیر محاسبه می شود:
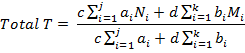
در برنامه پیش فرض ضریب دروس عمومی 1 و ضریب اختصاصی 3 می باشد که می توانید آن را برای هر آزمون تغییر دهید. -
مفهوم تراز
هر چند درصد، میزان پاسخ گویی یک دانش آموز به سوالات یک درس را مشخص می کند ولی از وضعیت آن دانش آموز در مقایسه با سایر داوطلبان اطلاعاتی به ما نمی دهد.
این مطلب را با یک مثال توضیح می دهم:
فرض کنید فرزندتان که همواره در مدرسه نمرات عالی داشته، در یک امتحان نمره ۱۵ کسب میکند،
آیا فرزندتان در این درس کم کاری کرده و سزاوار تنبیه است؟!
به لیست نمرات زیر دقت کنید:
۸،۹،۱۰،۱۱،۱۲،۱۲،۱۳،۱۳،۱۴،۱۵
اگر وضعیت نمرات همکلاسی های فرزندتان در آن امتحان شبیه لیست بالا باشد در واقع فرزند شما در مقایسه با بقیه بیشترین نمره را کسب کرده و در وضعیتی عالی قرار دارد و شایسته تشویق است حال آنکه شاید نمره ۱۵ ایشان در نگاه اول در مقایسه با نمرات امتحانات گذشته اش قابل قبول نباشد.
حال چنانچه لیست نمرات همکلاسی های فرزندتان به این شکل باشد:
۱۹/۷۵،۲۰،۲۰،۲۰،۲۰،۲۰،۲۰،۲۰،۲۰،۲۰
و نمره فرزند شما ۱۹/۷۵ باشد،
آیا این نمره بیانگر وضعیت عالی ایشان در کلاس است؟!
در واقع درصد هر دانش آموز در آزمون ها فقط میزان پاسخ گویی به سوالات آن درس را مشخص می کند و اطلاعاتی از سختی یا راحتی سوالات و میزان پاسخ گویی سایر شرکت کنندگان در اختیار ما نمی گذارد.
پس با اطلاع از درصد (نمره) نمی توان به جایگاه واقعی هر دانش اموز در هر درس رسید.
حال تصور کنید در یک آزمون تستی فرزندتان در درس۱ نمره ۷۰% و در درس۲ نمره۵۰% را کسب کرده باشد.
آیا درست است که بگویم ایشان در درس۲ ضعیف تر از درس۱ عمل کرده است؟
به لیست نمرات سایر دانش آموزان در دروس۱و۲ دقت کنید:
درس۱:
۷۰،۸۰،۹۰،۹۰،۱۰۰،۱۰۰،۱۰۰،۱۰۰،۱۰۰،۱۰۰
درس۲:
۰،۰،۰،۰،۱۰،۱۰،۲۰،۲۰،۲۰،۵۰
هر چند فرزند شما در درس۱ میزان پاسخ گویی بالایی به سوالات داشته اما نمره۵۰ ایشان در درس۲ ارزش بیشتری دارد چرا که در مقایسه با سایرین درصد پاسخ گویی چشم گیرتری است.
احتمالا سوالات درس۱ آسان تر از درس۲ طراحی شده و به همین علت پاسخ گویی دانش آموزان به سوالات این درس بالاتر بوده است.
در آزمون ها برای اینکه بتوانند وضعیت درستی از جایگاه فرد نسبت به بقیه ارائه کنند شاخصی به نام تراز معرفی کرده که این شاخص آماری، از روی درصد هر دانش آموز و با مقایسه آن با میانگین و نمرات سایر شرکت کنندگان محاسبه می شود. -
ضریب دشواری
در این روش ابتدا شرکت کنندگان را با توجه به نمره کل هر درس در آن آزمونرا به دو گروه قوی(بالا) و ضعیف (پایین) تقسیم می کنیم.
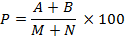
A : انتخاب های درست گروه قوی
B : انتخاب های درست گروه ضعیف
M : تعداد شرکت کنندگان گروه قوی
N : تعداد شرکت کنندگان گروه ضعیف
ضریب دشواری هر چه به سمت صفر میل کند به معنی دشواری زیاد سوال می باشد و هر چه به سمت 100 پیش برود به معنی آسانی سوال می باشد. به طور کلی، ضریب دشواری بین 30 تا 70 حداکثر اطلاع را درباره تفاوت بین آزمون شوندگان به دست می دهند.تفسیر ضریب دشواری سوال
در آزمون های هنجاری مثل آزمون هوش یا کنکور دانشگاه ، می توان واریانس سوال را مشخص کنیم . واریانس یک شاخص جهت نمایش پراکندگی نمرات در یک پیوستار ، به دست می دهد که در یک آزمون یا وضعیت هنجاری ، هرچه مقدار آن بیشتر باشد ، آزمودنی ها و افراد نمونه ، عملکرد مناسب تری داشته اند . در مورد پرسش های آزمون نیز ، هر چه واریانس بیشتر باشد ، سوال عملکرد بهتری داشته است .
-
ضریب تمییز
در این روش ابتدا شرکت کنندگان را با توجه به نمره کل هر درس در آن آزمون را به دو گروه قوی(بالا) و ضعیف (پایین) تقسیم می کنیم.
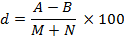
A : انتخاب های درست گروه قوی
B : انتخاب های درست گروه ضعیف
M : تعداد شرکت کنندگان گروه قوی
N : تعداد شرکت کنندگان گروه ضعیف
هر قدر ضریب تمییز بزرگتر باشد، قوه تشخیص آن سوال بیشتر و هر قدر این ضریب کوچک تر باشد، قوه تمییز آن کمتر است. به طور مثال اگر ضریب 91 باشد، آن سوال شرکت کنندگان قوی و ضعیف را خیلی خوب از هم جدا خواهد کرد. اما اگر ضریب تمییز 10 باشد، آن سوال از عهده جدا سازی شرکت کنندگان ضعیف و قوی به خوبی بر نخواهد آمد. این مشکل به طور معمول، به ایراد خود سوال مربوط بوده وباید اصلاح شود وچنانچه سوال دارای اشکال فنی نباشد، افراد گروه بالا یا آن سوال را به طورکامل یاد نگرفته اند یا آن را به غلط آموخته اند. بنابراین تمامی ضرایب تمییزآزمون باید مثبت باشد.
تحلیل گزینه های انحرافی
در گزینه های انحرافی قاعده کلی به شرح زیر است : هر گزینه ی انحرافی باید دست کم یک نفرازافراد گروه ضعیف را به خود جلب کند واگر هردوگروه قوی و ضعیف را به خود جلب کند ، تعداد افراد گروه ضعیف بیشتر ازگروه قوی باشد . بنابراین در صورتی یک سوال به خوبی عمل می کند که افراد گروه ضعیف بیشتر از افراد گروه قوی گزینه های انحرافی آن سوال را انتخاب نمایند . چنانچه گزینه ی انحرافی خاصی وجود داشته باشد که هیچ یک از افراد گروه قوی وضعیف آن را انتخاب نکرده باشند ، گزینه ی انحرافی مناسبی نیست وباید اصلاح شود .
-
کارنامه بدون غلط / کارنامه های بدون غلط
یکی از کارکرد های اصلی آزمون های آزمایشی شناخت ایرادها و نقطه ضعف هایی است که در پروسه مطالعه یا آزمون دادن هر شرکت کننده وجود دارد.
در واقع هر فرد با بررسی کارنامه و تحلیل صحیح آزمون های آزمایشی می تواند از این مشکلات مطلع و با اصلاح روش مطالعه یا پاسخ گویی، نسبت به رفع این موارد اقدام نماید.
دانش آموزان بسیاری وجود دارند که در مراجعات خود برای مشاوره عنوان می کنند برای یک آزمون زحمت زیادی کشیدند و تقریبا تمام منابع آزمون خوانده اند ولی متاسفانه به جای کسب تراز بهتر، تراز بدتری کسب کردند.
این افراد کورسوری امیدی را هم که با افزایش میزان مطالعه داشته اند از دست می دهند و ناامید از کسب نتیجه درس خواندن را رها میکنند.
ریشه مشکل این افراد در چیست؟ آیا واقعا مطالعه باعث کاهش تراز آنها شده است؟
واضح است که پاسخ این سوال خیر است.
یکی از دلایل عمده که باعث کاهش تراز این افراد می شود مطالعه ناقص منابع آزمون است.
در هفته هایی که دانش اموز مطالعه چندانی ندارد و تمام هم و غم خود را روی یک یا دو مبحث از هر درس می گذارد سر جلسه آزمون سوالات مابقی مباحث را رها کرده و تمام وقت و انرژی خود را صرف سوالات همان یک یا دو مبحث میکند.
طبیعتا در این حالت تایم بیشتری برای پاسخ گویی به سوالات مورد نظر داشته و به تعدادی از آنها هم پاسخ صحیح میدهد.
اما در آزمون هایی که به اظهار خودش، تمامی منابع را به اتمام رسانده، تصور میکند باید به تمامی سوالات پاسخ دهد حال آنکه شاید خیلی از مباحث را به صورت ناقص مطالعه کرده و یا فقط به خواندن درسنامه اکتفا نموده و تعداد تست و تمرین ناچیزی از آنها حل کرده است.
در این حالت به نسبت حالت قبلی، تایم کمتری هم برای پاسخ گویی به سوالات در اختیار دارد چون در تایم آزمون، خود را موظف می داند که به تمامی سوالات پاسخ دهد بنابر این مجبور است فرایند پاسخ گویی را سریع تر انجام دهد.
این موارد دست به دست هم داده و باعث افزایش تعداد غلط های دانش آموز می شود و از آنجا که سوالات غلط در آزمون ها نمره منفی دارد باعث کاهش درصد و در نهایت کاهش تراز ایشان می شود.
خوشبختانه با امکانی که اخیرا به نرم افزار تصحیح تست هوشمند آسا اضافه شده، در کارنامه دانش آموز درصد، تراز و رتبه در حالت بدون_غلط نیز درج می شود.
نرم افزار در این حالت تمامی پاسخ های غلط دانش آموز رو نادیده گرفته (به نزده تبدیل می کند و نه به درست) و درصد بدون غلط ایشان را به دست می آورد. سپس از روی درصد بدون غلط هر دانش اموز و درصد های عادی (همراه با غلط) سایر شرکت کنندگان تراز بدون غلط را برای هر درس این دانش آموز محاسبه (و همچنین رتبه جدید در همین آزمون محاسبه می شود) و در نهایت از روی تراز بدون غلط دروس تراز ها و رتبه های عمومی، اختصاصی و کل را محاسبه میکند.
این درصد و تراز و رتبه بدون غلط خیلی مهم و ارزشمند است.
چرا که دانش آموز با مقایسه درصد و تراز و رتبه در دوحالت با و بدون غلط می تواند بهتر و بیشتر مفهوم نمره منفی رو درک و مِن بعد تمام تلاش خود را بکار میگیرد تا در آزمون های بعدی پاسخ منفی کمتری داسته باشد و با ارزیابی و تحلیل آزمون همین اشتباهات را به پاسخهایی درست در آزمونهای آینده تبدیل می کند.
با این کار، هم آزمون را ارزیابی کرده و یادگیریاش کامل شده و هم تراز و رتبه اش افزایش خوبی داشته است؛ بنابراین از هر دو جهت برنده است. پاسخهای اشتباه همان پاسخهای درستی هستند که دانشآموز قرار است با ارزیابی آن در آزمون بعدی به آنها برسد. به همین دلیل است که میگویند «پاسخهای اشتباه را باید دوست داشت.»
دانشآموزان بدانند که آزمون وقتی به سرانجام میرسد که ارزیابی آن را تمام و کمال انجام دهند.
شاید این بهترین روشی باشد که بتوانید به دانش آموزانی که بی پروا غلط میزنن اهمیت غلط نزدن را بیاموزید و شاید یک همچین کارنامه ایی برابر با دو تا سه جلسه مشاوره باشد
مشاهده نمونه کارنامه بدون غلط
مشاهده فیلم نحوه استفاده از کارنامه بدون غلط در آسا
در این فیلم انواع گزارشهای بدون غلط را برای کارنامه های فردی، گزارش های گروهی مدیریتی و گزارش های تک درس برای دبیران را می توانید مشاهده کنید